| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- MySQL
- typeORM
- class
- MongoDB
- flask
- 자료구조
- AWS
- cookie
- OCR
- game
- JavaScript
- Nest.js
- 정렬
- Python
- Queue
- jest
- nodejs
- 게임
- Dinosaur
- TypeScript
- react
- nestjs
- Sequelize
- dfs
- mongoose
- 공룡게임
- GIT
- Bull
- Express
- Today
- Total
포시코딩
탐욕 알고리즘(Greedy Algorithm) 본문
탐욕 알고리즘이란?
- 최적의 해에 가까운 값을 구하기 위해 사용
- 여러 경우 중 하나를 결정해야 할 때마다, 매 순간 최적이라고 생각되는 경우를 선택하는 방식으로 진행하여
최종적인 값을 구하는 방식
예시 문제
문제 1. 동전 문제
지불해야 하는 값이 4720원일 때 10원, 50원, 100원, 500원 동전으로 동전의 수가 가장 적게 지불하시오.
- 가장 큰 동전부터 최대한 지불하는 방법으로 구현 가능
- 탐욕 알고리즘으로 매 순간 최적이라고 생각되는 경우를 선택
코드
coin_list = [500, 100, 50, 10]
def min_coin_count(value, coin_list):
total_coin_count = 0
details = list()
coin_list.sort(reverse=True) # 큰 순서로 정렬
for coin in coin_list:
coin_num = value // coin
total_coin_count += coin_num
value -= coin_num * coin
details.append([coin, coin_num])
return total_coin_count, details
result = min_coin_count(4720, coin_list)
print(result)
문제 2. 부분 배낭 문제(Fractional Knapsack Problem)
무게 제한이 K인 배낭에 최대 가치를 가지도록 물건을 넣는 문제

- 각 물건은 무게(w)와 가치(v)로 표현된다.
- 물건은 쪼갤 수 있으므로 물건의 일부분만 배낭에 넣을 수 있다. (-> Fractional Knapsack Problem이라 부르는 이유)
* 반대로 물건을 쪼갤 수 없는 배낭 문제도 존재 (-> 0/1 Knapsack Problem이라 부름)
코드
data_list = [(10, 10), (15, 12), (20, 10), (25, 8), (30, 5)]표에 나온 물건들에 대해 list화 시키면 위와 같다.
무게 당 가치를 sorted() 함수와 lambda 옵션을 통해 정렬하면 아래와 같다.
data_list = sorted(data_list, key=lambda x: x[1] / x[0], reverse=True)
print(data_list) # 무게 단위 당 가치로 높은것부터 정렬
# [(10, 10), (15, 12), (20, 10), (25, 8), (30, 5)]이를 통해 아래와 같이 구현할 수 있다.
data_list = [(10, 10), (15, 12), (20, 10), (25, 8), (30, 5)]
def get_max_value(data_list, k):
data_list = sorted(data_list, key=lambda x: x[1] / x[0], reverse=True)
total_value = 0
details = list()
for data in data_list:
if k - data[0] >= 0: # 0 미만일 경우: 배낭 가용 무게가 5만 남았는데 무게가 10인 물건의 경우 쪼개서 넣기 위함
k -= data[0]
total_value += data[1]
details.append([data[0], data[1], 1]) # 3번째 인자 1은 100% 다 온전한 상태로 넣었다는 뜻
else:
fraction = k / data[0]
# k -= data[0] * fraction
# 굳이 안쓰는 이유는 else로 넘어와 해당 로직이 수행될 때 남은 부분에 대해 이미 쪼개서 넣는 상황이기 때문에
# 남은 무게는 0이 되어 계산할 필요가 없어진다.
total_value += data[1] * fraction
details.append([data[0], data[1], fraction])
break
return total_value, details
result = get_max_value(data_list, 30)
print(result)
단점
탐욕 알고리즘에는 한계가 있는데 다음과 같다.
- 탐욕 알고리즘은 근사치 추정에 활용
- 반드시 최적의 해를 구할 수 있는 것은 아니기 때문
- 최적의 해에 가까운 값을 구하는 방법 중 하나
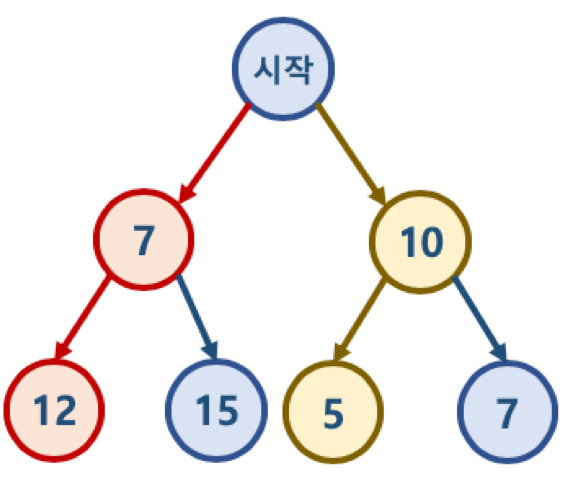
예로 위 사진에서 시작에서 출발하여 합이 최소가 되는 경우를 찾으라고 할 때,
탐욕 알고리즘을 쓴다면 7부터 선택하여 결국 19가 된다.
하지만 10 -> 5 를 선택할 경우 15로 더 작은 결과를 얻을 수 있다.
이처럼 매 순간의 최적의 값이 전체의 최적의 값과 다른 경우들이 존재할 수 있기 때문에
탐욕 알고리즘은 근사치 추정에 활용되지만 그 자체가 최적의 값을 보장하진 않는다는 점을 명심해야 한다.
활용
그렇다면 이걸 어디에 쓸 수 있을까?
탐욕 알고리즘을 활용해 푸는 문제를 보며 패턴을 익히며 어떻게 쓸지 알아보자
https://www.acmicpc.net/problem/11399
11399번: ATM
첫째 줄에 사람의 수 N(1 ≤ N ≤ 1,000)이 주어진다. 둘째 줄에는 각 사람이 돈을 인출하는데 걸리는 시간 Pi가 주어진다. (1 ≤ Pi ≤ 1,000)
www.acmicpc.net
우리가 위에서 예시 문제들을 볼 때 패턴을 알 수 있는데
정렬 -> 데이터 처리
의 과정을 거치고 있다.
정렬 후 시간이 적게 걸리는 사람부터 ATM을 사용하면서 기다린 시간들을 더한 값을 리턴하면 된다.
코드로 구현하면 다음과 같다.
N = int(input())
P = list(map(int, input().split()))
P.sort()
total = 0
for x in range(N):
for y in range(x+1):
total += P[y]
print(total)
탐욕 알고리즘을 배우며 든 생각인데
이건 특별하게 '사용'하는 것이 아닌 '방법'중 하나라
지금까지 나도 알게 모르게 써오지 않았을까 싶었다.
이름도 그렇고 옛날부터 굉장히 궁금해하면서 얼마나 대단한 알고리즘일까 싶었는데
막상 까보니 그렇게 특별하진 않은 느낌
근데 그렇기에 이걸 다른 알고리즘과 같이 활용해 더더욱 좋은 시너지를 낸다고 하니
앞으로의 활용방법이 매우 기대된다.
'자료구조알고리즘 > 이론' 카테고리의 다른 글
| 소수찾기 - 에라토스테네스의 체 (0) | 2023.04.16 |
|---|---|
| [완전탐색] 순열과 조합 - 복습필요 (0) | 2023.04.15 |
| 그래프 - DFS 구현 (1) | 2023.04.15 |
| 그래프 - BFS 구현 (1) | 2023.04.15 |
| 그래프 - BFS, DFS 개념 (0) | 2023.04.14 |




