Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- typeORM
- JavaScript
- 공룡게임
- Nest.js
- 정렬
- AWS
- game
- dfs
- OCR
- react
- Sequelize
- 자료구조
- Queue
- Dinosaur
- nestjs
- MySQL
- Express
- TypeScript
- class
- flask
- 게임
- Python
- MongoDB
- cookie
- GIT
- Bull
- nodejs
- mongoose
- jest
Archives
- Today
- Total
포시코딩
그래프 - 최단 경로 알고리즘, 다익스트라 알고리즘 본문
728x90
최단 경로 문제란?
- 두 노드를 잇는 가장 짧은 경로를 찾는 문제
- 가중치 그래프(Weighted Graph)에서 간선(Edge)의 가중치 합이 최소가 되도록 하는 경로를 찾는 것이 목적
문제 종류
단일 출발 및 단일 도착
- 그래프 내의 특정 노드 u에서 출발, 또 다른 특정 노드 v에 도착하는 가장 짧은 경로를 찾는 문제
단일 출발
- 그래프 내의 특정 노드 u와 그래프 내 다른 모든 노드 각각의 가장 짧은 경로를 찾는 문제
- 출발점이 A라고 한다면 A가 아닌 각각 다른 노드들 간의 최단 경로를 찾는걸 의미
- 다익스트라 알고리즘이 여기에 해당됨
전체 쌍(all-pair)
- 그래프 내의 모든 노드 쌍(u, v)에 대한 최단 경로를 찾는 문제
다익스트라 알고리즘
- 첫 정점을 기준으로 연결되어 있는 정점들을 추가해가며 최단 거리를 갱신하는 기법
- 너비우선탐색(BFS)와 유사하다.
- 우선순위 큐를 사용하는 방법이 제일 개선된 방법이다.
* MinHeap 방식을 활용하여 현재 가장 짧은 거리를 가진 노드 정보를 먼저 꺼냄
구현
초기화
- 출발노드와 각 노드들간에 거리를 저장할 수 있는 배열을 선언
* 출발노드(자신)와의 거리는 0, 나머지는 아직 모르니 inf(무한대)로 저장 - 우선순위 큐에 (첫 정점, 거리 0)만 먼저 넣는다.
반복
- 우선순위 큐에서 노드를 꺼낸다.
* 처음에는 첫 정점만 저장되어 있으므로, 첫 정점이 꺼내짐 - 꺼낸 노드와 인접한 노드들 각각에 대한 거리와 배열에 저장된 거리를 비교하여
배열에 저장된 거리보다 더 짧을 경우 배열에 해당 노드의 거리를 업데이트한다. - 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
* 이럴경우 BFS와 유사하게 첫 정점에 인접한 노드들을 우선 순차적으로 방문
탈출
우선순위 큐에 꺼낼 노드가 없을 때 까지 위 반복 과정을 수행한다.
과정

mygraph = {
'A': {'B': 8, 'C': 1, 'D': 2},
'B': {},
'C': {'B': 5, 'D': 2},
'D': {'E': 3, 'F': 5},
'E': {'F': 1},
'F': {'A': 5}
}1 단계
초기화: 첫 정점을 기준으로 배열을 선언하여 첫 정점에서 각 정점까지의 거리를 저장
- 첫 정점의 거리는 0, 나머지는 inf(무한대)로 저장
- 우선순위 큐에 (첫 정점, 거리 0) 먼저 넣음

2 단계
우선순위 큐에서 추출한 (A, 0) [노드, 첫 노드와의 거리]를 기반으로 인접한 노드와의 거리 계산
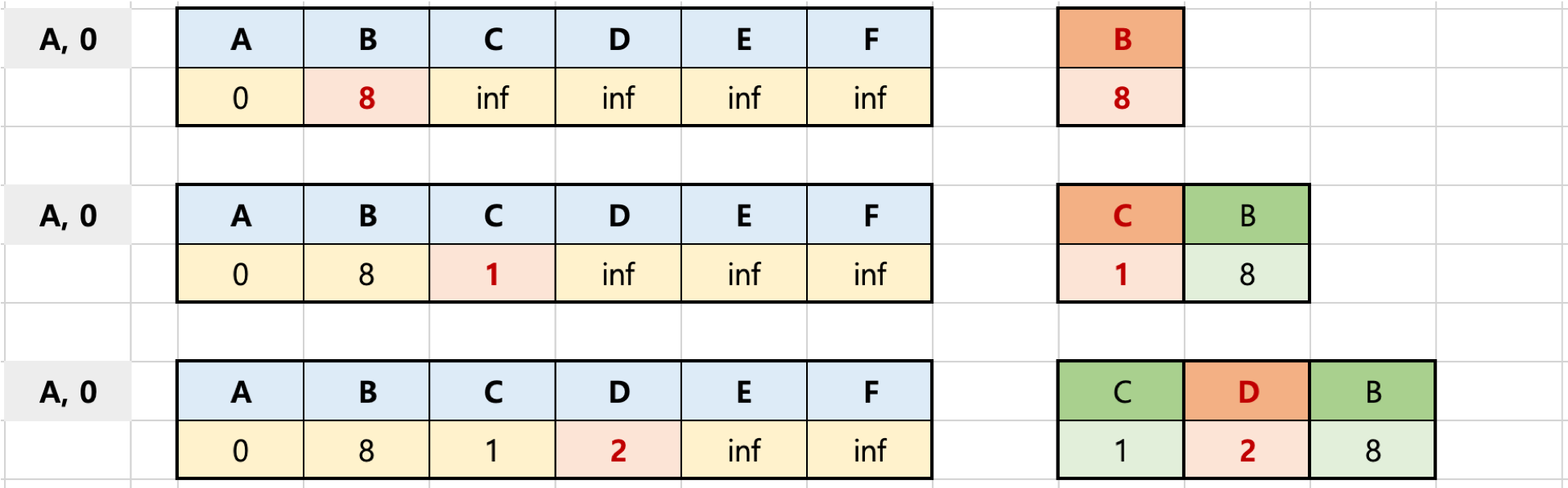
- 우선순위 큐에서 노드를 꺼냄
- 처음에는 첫 정점만 저장되어 있으므로 첫 정점이 꺼내짐 -> A, 0
- 첫 정점에 인접한 노드들 각각에 대해 첫 정점에서 각 노드로 가는 거리와
현재 배열에 저장되어 있는 첫 정점에서 각 정점까지의 거리를 비교한다.
-> 'A': {'B': 8, 'C': 1, 'D': 2} - 배열에 저장된 거리보다 첫 정점에서 해당 노드로 가는 거리가 더 짧을 경우 배열에 해당 노드의 거리를 업데이트
- 배열에 해당 노드의 거리가 업데이트된 경우, 우선순위 큐에 넣는다.
* 결과적으로 BFS와 유사하게 첫 정점에 인접한 노드들을 순차적으로 방문
* 만약 배열에 기록된 현재까지 발견된 거리보다 더 긴 거리를 가진 노드일 경우 2번 순서의 비교를 하지않고 패스
3단계
우선순위 큐에서 추출한 (C, 1) [노드, 첫 노드와의 거리]를 기반으로 인접한 노드와의 거리 계산

- 우선순위 큐가 MinHeap(최소 힙) 방식이므로, 위 표에서 넣어진 (C, 1), (D, 2), (B, 8) 중 (C, 1)이 먼저 추출된다.(pop)
-> 'C': {'B': 5, 'D': 2} - 이전 단계까지의 A - B 최단 거리는 8인 상황
- A - C 최단거리는 1, C - B 최단거리는 5. 즉, A - C - B의 최단거리는 1 + 5 = 6이므로
A - B 최단거리 8보다 더 작기 때문에 이를 배열에 업데이트 한다. (위 사진 참고) - 배열에 해당 노드의 거리가 업데이트 됐으므로 (B, 6) 값이 우선순위 큐에 넣어짐
- A - C 최단거리는 1, C - B 최단거리는 5. 즉, A - C - B의 최단거리는 1 + 5 = 6이므로
- C - D의 최단거리는 2, A - C - D의 최단거리는 1 + 2 = 3이므로
A - D의 최단거리 2보다 길기 때문에 업데이트 되지 않는다.
4단계
우선순위 큐에서 추출한 (D, 2) [노드, 첫 노드와의 거리]를 기반으로 인접한 노드와의 거리 계산

- 'D': {'E': 3, 'F': 5}
- A - D의 거리 2 + D - E의 거리 3 = 5 -> (E, 5) 업데이트 -> 우선순위 큐에 추가
- A - D의 거리 2 + D - F의 거리 5 = 7 -> (F, 7) 업데이트 -> 우선순위 큐에 추가
5단계
우선순위 큐에서 추출한 (E, 5) [노드, 첫 노드와의 거리]를 기반으로 인접한 노드와의 거리 계산

- -> 'E': {'F': 1}
- A - E의 거리 5, E - F의 거리 1. 즉, A - E - F의 거리 5 + 1 = 6
이전 단계 기준 (F, 7)이었으므로 (F, 6)으로 업데이트 및 우선순위 큐에 추가
- A - E의 거리 5, E - F의 거리 1. 즉, A - E - F의 거리 5 + 1 = 6
6단계
우선순위 큐에서 추출한 (B, 6), (F, 6)를 순차적으로 추출해 인접한 노드와의 거리 계산

- 'B': {}
- B 노드는 다른 노드로 가는 루트가 없어서 패스
- 'F': {'A': 5}
- F 노드는 A로 가는 루트가 있으나 현재 A - A가 0인 반면, A - F - A는 6 + 5 = 11
즉, 더 긴 거리이므로 업데이트 되지 않는다.
- F 노드는 A로 가는 루트가 있으나 현재 A - A가 0인 반면, A - F - A는 6 + 5 = 11
7단계
우선순위 큐에서 추출한 (F, 7), (B, 8)를 순차적으로 추출해 인접한 노드와의 거리 계산

- (F, 7), (B, 8) 둘 다 이미 배열에 최단거리가 더 짧은게 저장되어 있으므로 계산할 필요 없이 패스된다.
우선순위 큐 장점
- 지금까지 발견된 가장 짧은 거리의 노드에 대해 먼저 계산
- 더 긴 거리로 계산된 루트에 대해서는 계산을 스킵할 수 있다.
코드
import heapq
def dijkstra(graph, start):
distances = { node: float('inf') for node in graph }
distances[start] = 0
queue = []
heapq.heappush(queue, [distances[start], start])
while queue:
current_distance, current_node = heapq.heappop(queue)
if distances[current_node] < current_distance:
continue
for adjacent, weight in graph[current_node].items():
distance = current_distance + weight
if distance < distances[adjacent]:
distances[adjacent] = distance
heapq.heappush(queue, [distance, adjacent])
return distances
mygraph = {
'A': {'B': 8, 'C': 1, 'D': 2},
'B': {},
'C': {'B': 5, 'D': 2},
'D': {'E': 3, 'F': 5},
'E': {'F': 1},
'F': {'A': 5}
}
print(dijkstra(mygraph, 'A'))
# {'A': 0, 'B': 6, 'C': 1, 'D': 2, 'E': 5, 'F': 6}
시간복잡도
다익스트라 알고리즘은 크게 다음 두 가지 과정을 거친다.
- 과정 1: 각 노드마다 인접한 간선들을 모두 검사
- 과정 2: 우선순위 큐에 노드/거리 정보를 넣고 삭제(pop)
각 과정 별 시간복잡도
- 과정 1: 각 노드는 최대 한 번씩 방문하므로, 그래프의 모든 간선은 최대 한 번씩 검사
즉, 각 노드마다 인접한 간선들을 모두 검사하는 과정은 O(E) 시간이 걸린다. (E는 Edge) - 과정 2: 검사할 때마다 최단거리라 배열을 업데이트 시키고 우선순위 큐에 추가하는 경우 최악의 시간이 걸림
- 이 때, 추가는 각 간선마다 최대 한 번 일어날 수 있기 때문에 최대 O(E)의 시간이 걸린다.
- O(E)개의 노드/거리 정보에 대해 우선순위 큐를 유지하는 작업은 O(logE)의 시간이 걸린다.
- 따라서, 과정 2에 걸리는 시간은 O(ElogE)가 된다.
총 시간복잡도
과정 1 + 과정 2 = O(E) + O(ElogE) = O(E + ElogE) = O(ElogE)
예시 문제
https://www.acmicpc.net/problem/10282
10282번: 해킹
최흉최악의 해커 yum3이 네트워크 시설의 한 컴퓨터를 해킹했다! 이제 서로에 의존하는 컴퓨터들은 점차 하나둘 전염되기 시작한다. 어떤 컴퓨터 a가 다른 컴퓨터 b에 의존한다면, b가 감염되면
www.acmicpc.net
node가 숫자일 때
import heapq
def dijkstra(start):
distances = [float('inf')] * (n+1)
distances[start] = 0
queue = []
heapq.heappush(queue, (0, start))
while queue:
curr_distance, curr_node = heapq.heappop(queue)
if distances[curr_node] < curr_distance:
continue
for n_node, n_distance in graph[curr_node]:
distance = curr_distance + n_distance
if distances[n_node] > distance:
distances[n_node] = distance
heapq.heappush(queue, (distance, n_node))
return distances
for _ in range(int(input())):
n, d, start = map(int, input().split())
graph = [[] for _ in range(n+1)]
for _ in range(d):
a, b, s = map(int, input().split())
graph[b].append((a, s))
result = dijkstra(start)
count = 0
max_distance = 0
for i in result:
if i != float('inf'):
count += 1
max_distance = max(max_distance, i)
print(count, max_distance)
node가 문자일 때
import heapq
def dijkstra(start):
distances = { node: float('inf') for node in graph }
distances[start] = 0
queue = []
heapq.heappush(queue, [distances[start], start])
while queue:
curr_distance, curr_node = heapq.heappop(queue)
if distances[curr_node] < curr_distance:
continue
for n_node, n_distance in graph[curr_node].items():
distance = curr_distance + n_distance
if distance < distances[n_node]:
distances[n_node] = distance
heapq.heappush(queue, [distance, n_node])
return distances
for _ in range(int(input())):
n, d, start = map(int, input().split())
graph = { computer: {} for computer in range(1, n+1) }
for _ in range(d):
a, b, s = map(int, input().split())
graph[b][a] = s
result = dijkstra(start)
count = 0
max_distance = 0
for i in result:
if result[i] != float('inf'):
count += 1
max_distance = max(max_distance, result[i])
print(count, max_distance)728x90
'자료구조알고리즘 > 이론' 카테고리의 다른 글
| 최소 신장 트리(Minimum Spanning Tree, MST) (0) | 2023.04.18 |
|---|---|
| 백트래킹(backtracking) (0) | 2023.04.16 |
| 알고리즘 코딩테스트를 대비해 외울 것들 (0) | 2023.04.16 |
| 소수찾기 - 에라토스테네스의 체 (0) | 2023.04.16 |
| [완전탐색] 순열과 조합 - 복습필요 (0) | 2023.04.15 |



