Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- Bull
- OCR
- flask
- Queue
- mongoose
- 자료구조
- Express
- GIT
- class
- typeORM
- game
- nestjs
- MongoDB
- jest
- Sequelize
- MySQL
- TypeScript
- AWS
- JavaScript
- Python
- Nest.js
- 공룡게임
- Dinosaur
- dfs
- react
- cookie
- 게임
- nodejs
- 정렬
Archives
- Today
- Total
포시코딩
백트래킹(backtracking) 본문
728x90
백트래킹이란?
- 백트래킹 또는 퇴각검색이라고 불린다.
- 기법의 한 종류
- 제약 조건 만족 문제(Constraint Satisfaction Problem)에서 해를 찾기 위한 전략
- 해를 찾기 위해, 후보군에 제약 조건을 점진적으로 체크하다가, 해당 후보군이 제약 조건을 만족할 수 없다고 판단되는 즉시
backtrack하고, 바로 다른 후보군으로 넘어가며 결국 최적의 해를 찾는 방법
- 해를 찾기 위해, 후보군에 제약 조건을 점진적으로 체크하다가, 해당 후보군이 제약 조건을 만족할 수 없다고 판단되는 즉시
- 실제 구현 시, 고려할 수 있는 모든 경우의 수(후보군)를 상태 공간 트리(State Space Tree)를 통해 표현한다.
- 각 후보군을 DFS 방식으로 확인
- 상태 공간 트리를 탐색하면서, 제약이 맞지 않으면 해의 후보가 될만한 곳으로 바로 넘어가서 다시 탐색
- Promising: 해당 루트가 조건에 맞는지 검사하는 기법
- Pruning(가지치기): 조건에 맞지 않다면 포기하고 다른 루트로 바로 돌아서서 탐색의 시간을 절약하는 기법
상태 공간 트리란?
문제 해결 과정의 중간 상태를 각각의 노드로 나타낸 트리

예시 문제: N Queen 문제
- 대표적인 백트래킹 문제
- N x N 크기의 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치하는 문제
- 퀸은 다음과 같이 이동할 수 있으므로, 배치된 퀸 간에 공격할 수 없는 위치로 배치해야 한다.

Pruning
- 한 행에는 하나의 퀸 밖에 위치할 수 없다.(퀸은 수평 이동이 가능하므로)
- 맨 위에 있는 행부터 퀸을 배치하고, 다음 행에 해당 퀸이 이동할 수 없는 위치를 찾아 퀸을 배치
- 만약 앞선 행에 배치한 퀸으로 인해, 다음 행에 해당 퀸들이 이동할 수 없는 위치가 없을 경우에는
더 이상 퀸을 배치하지 않고 이전 행의 퀸의 배치를 바꾼다.- 즉, 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후
각 경우를 맨 위의 행부터 DFS 방식으로 접근, 해당 경우가 진행이 어려울 경우 더 이상 진행하지 않고 다른 경우를 체크한다.
- 즉, 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후

Promising
- 해당 루트가 조건에 맞는지를 검사하는 기법을 활용
- 현재까지 앞선 행에서 배치한 퀸이 이동할 수 없는 위치가 있는지를 다음과 같은 조건으로 확인한다.
- 한 행에 어차피 하나의 퀸만 배치가 가능하므로 수평 체크는 필요하지 않음
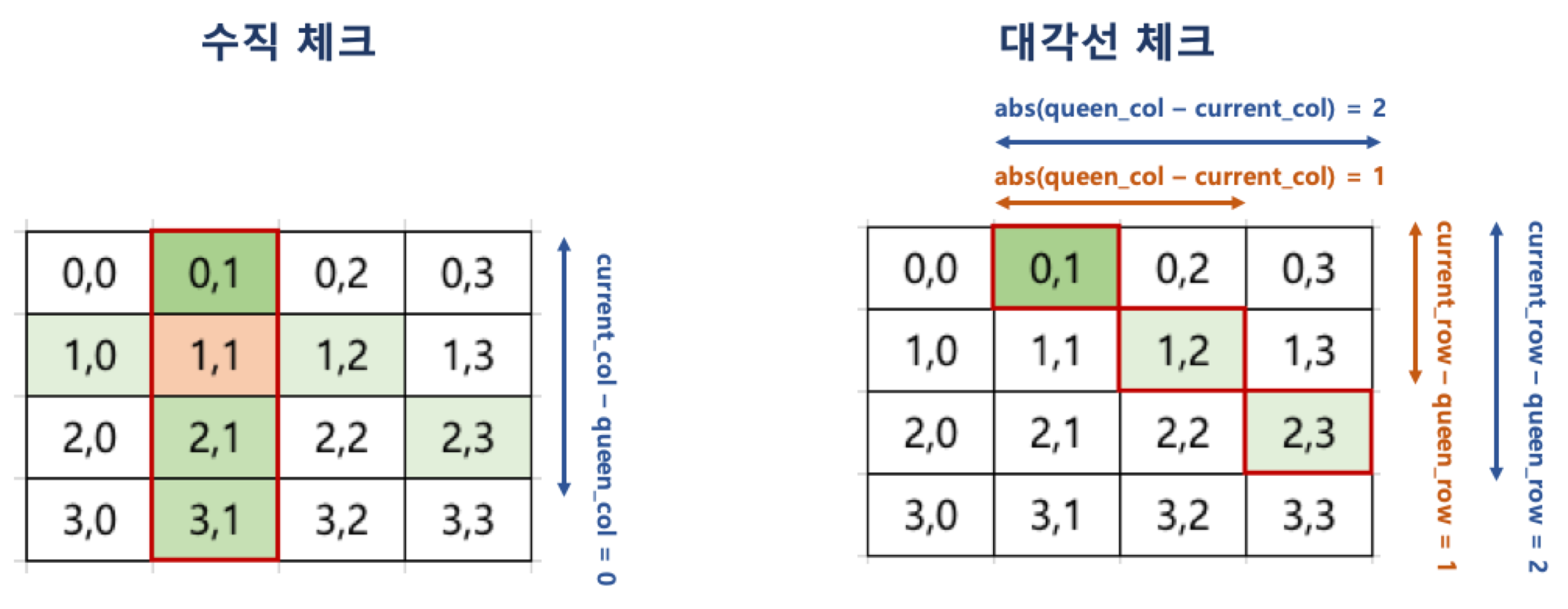
수직 체크
열이 같은지만 체크
current_col == queen_col이 경우 같은 열에 위치하므로 다음 퀸이 위치할 수 없다.
대각선 체크
행의 갭과 열의 갭이 같은지를 체크
- 행의 갭: 현재 행이 항상 더 크므로 현재 행 - 퀸의 행을 하면 나온다.
- 열의 갭: 왼쪽에도, 오른쪽에도 있을 수 있으므로 그 갭의 abs(절대값)을 구한다.
current_row - queen_row = 1
abs(queen_col - current_col) = 1
# 즉, 아래와 같이 나타낼 수 있다.
abs(queen_col - current_col) == current_row - queen_row이 경우 대각선에 위치하므로 다음 퀸이 위치할 수 없다.
코드
def is_available(candidate, current_col): # candidate -> index: 행, value: 열
current_row = len(candidate)
# candidate에는 이전 행들의 열 정보가 담겨있기 때문에 개수를 통해 현재 행의 위치를 알 수 있다.
for queen_row in range(current_row):
# [index, value]로 이전 queen들의 위치를 알 수 있다.
if candidate[queen_row] == current_col or abs(candidate[queen_row] - current_col) == current_row - queen_row:
return False
return True
def DFS(N, current_row, current_candidate, final_result):
if current_row == N:
final_result.append(current_candidate[:]) # list[:] -> 얇은 복사
return
# 현재 행에서 각각의 열에 대해 for문
for candidate_col in range(N):
# is_available에서 수직 체크, 대각선 체크 진행
if is_available(current_candidate, candidate_col):
current_candidate.append(candidate_col)
DFS(N, current_row + 1, current_candidate, final_result)
current_candidate.pop()
# 다음 진행한 DFS들이 is_available = False일 때
# 다음 열로 넘어가거나, 마지막 열이면 그 위의 행으로 올라감
def solve_n_queens(N):
final_result = []
DFS(N, 0, [], final_result)
return final_result
result = solve_n_queens(4)
print(result)
문제 & 개선된 코드
https://www.acmicpc.net/problem/9663
9663번: N-Queen
N-Queen 문제는 크기가 N × N인 체스판 위에 퀸 N개를 서로 공격할 수 없게 놓는 문제이다. N이 주어졌을 때, 퀸을 놓는 방법의 수를 구하는 프로그램을 작성하시오.
www.acmicpc.net
N-Queen 관련 문제가 백준에 있어서 가져왔다.
해당 문제에서는 퀸이 배치될 수 있는 경우의 배치도가 아닌 오로지 해당 경우의 수를 리턴하면 되기 때문에
두가지 방법으로 코드를 작성해봄
코드(퀸 배치 목록 포함)
def is_available(candidate, curr_col):
curr_row = len(candidate)
for queen_row in range(curr_row):
if candidate[queen_row] == curr_col:
return False
if abs(candidate[queen_row] - curr_col) == curr_row - queen_row:
return False
return True
def DFS(N, candidate):
global result
if len(candidate) == N:
result.append([*candidate])
for curr_col in range(N):
if is_available(candidate, curr_col):
candidate.append(curr_col)
DFS(N, candidate)
candidate.pop()
N = int(input())
result = []
DFS(N, [])
print(result)
print(len(result))
코드(경우의 수만)
def is_available(curr_row):
for queen_row in range(curr_row):
if candidate[curr_row] == candidate[queen_row]:
return False
if abs(candidate[curr_row] - candidate[queen_row]) == curr_row - queen_row:
return False
return True
def DFS(curr_row):
global result
if curr_row == N:
result += 1
else:
for curr_col in range(N):
candidate[curr_row] = curr_col
if is_available(curr_row):
DFS(curr_row+1)
N = int(input())
candidate = [0] * N
result = 0
DFS(0)
print(result)백트래킹을 사용할 일이 있을 때 위 두가지 방법을 떠올려 활용하면
경우의 수, 목록을 둘 다 가져와 사용할 수 있을 것이다.
* 참고로 퀸 배치 목록이 포함된 코드는 시간 초과가 난다. (진짜 살짝 경계에 걸친건지 정답처리될 때도 있음)
728x90
'자료구조알고리즘 > 이론' 카테고리의 다른 글
| [MST][최소 신장 트리] Kruskal's algorithm (0) | 2023.04.18 |
|---|---|
| 최소 신장 트리(Minimum Spanning Tree, MST) (0) | 2023.04.18 |
| 그래프 - 최단 경로 알고리즘, 다익스트라 알고리즘 (0) | 2023.04.16 |
| 알고리즘 코딩테스트를 대비해 외울 것들 (0) | 2023.04.16 |
| 소수찾기 - 에라토스테네스의 체 (0) | 2023.04.16 |



